Outil essentiel à la communication, la parole utilise les ondes sonores pour transporter l'information. Mais beaucoup ignorent cependant leur véritable nature.
Qu'est-ce qu'une onde sonore ?
I - Définition d'une onde sonore
Les ondes sonores sont des ondes longitudinales de compression dilatation, c'est-à-dire que la source de la perturbation se déplace dans la même direction que la propagation.
Physiquement, l'onde naît de la création de zones de pression et de dépression qui vont se propager dans une même direction, espacées d'intervalles de temps caractéristiques de fréquences utilisées.
L'onde peut ainsi se définir comme la propagation couplée de deux grandeurs : la vitesse et la pression.
II - Équations de propagation
Afin d'étudier au mieux les ondes sonores, nous sommes contraints de négliger certains phénomènes et de procéder à des approximations. Tout d'abord, on suppose le fluide parfait et les transformations adiabatiques réversibles : tous les phénomènes dissipatifs sont alors négligés.
D'autre part, on procède à l'approximation acoustique, qui consiste à ne garder que les terme d'ordre 1 pour la pression, la masse volumique et la vitesse.
Ainsi :
\[P \rightarrow P=P_{0}+P_{1}\]\[\mu \rightarrow \mu=\mu_{0}+\mu_{1}\] \[\overrightarrow{0} \rightarrow \overrightarrow{v}\]
L'objectif est de trouver l'équation régissant la propagation des ondes sonores, en passant par l'établissement de 3 équations intermédiaires qui, une fois combinées, nous amèneront au résultat.
\[P \rightarrow P=P_{0}+P_{1}\]\[\mu \rightarrow \mu=\mu_{0}+\mu_{1}\] \[\overrightarrow{0} \rightarrow \overrightarrow{v}\]
L'objectif est de trouver l'équation régissant la propagation des ondes sonores, en passant par l'établissement de 3 équations intermédiaires qui, une fois combinées, nous amèneront au résultat.
1 - Equation d'Euler :
\[\mu. [\frac{\partial \overrightarrow{v}}{\partial t}+[\overrightarrow{v}.\overrightarrow{grad}]\overrightarrow{v}]=\mu \overrightarrow{g}-\overrightarrow{grad}(P)\]
On néglige le poids (car les fréquences utilisées sont assez importantes).
En comparant les termes convectif et local, on s'aperçoit que l'accélération locale est également négligeable.
Et en travaillant à l'ordre 1, on établit donc la 1ère équation, notée (1) :\[\mu _{0}\frac{\partial \overrightarrow{v}}{\partial t}=-\overrightarrow{grad}(P)\]
2 - Conservation de la masse
On utilise la conversation de la masse en gardant tous les termes à l'ordre 1. On obtient alors l'équation (2) :\[\frac{\partial \mu }{\partial t}+\mu _{0}div(\overrightarrow{v})=0\]
3 - Transformation adiabatique et coefficient de compressibilité
On définit le coefficient de compressibilité isentropique par la relation suivante : \[\chi _{S}=\frac{1}{\mu}\frac{\partial \mu }{\partial P}\] Il vient alors la relation :\[\frac{d\mu }{\mu }=\chi _{S}.dP\] d'où :\[ln(\frac{\mu }{\mu _{0}})=\chi _{S}(P-P_{0})\]
III - Aspect énergétique
On en tire alors l'équation (3) donnée par : \[\mu _{1}=\mu _{0}\chi_{S}P_{1}\]
En combinant les 3 équations, on peut établir l'équation de propagation des ondes sonores dans un milieu fluide :\[\mu _{0\chi _{S}}\frac{\partial^2 P_{1}}{\partial t^2}=\Delta P_{1}\]
On reconnaît une équation de type d'Alembert (équation linéaire faisant intervenir des dérivées d'ordre 2 par rapport au temps et à l'espace). On s'y attendait un peu puisque nous avions négligé toute cause d'irréversibilité en supposant le fluide parfait et les transformations adiabatiques réversibles.
On peut dès lors poser la vitesse c définie par la relation : \[c=\frac{1}{\sqrt{\mu _{0}\chi _{S}}}\]
A 20°C, on trouve une vitesse d'environ 340m/s, ce qui correspond relativement bien aux résultats expérimentaux mesurés.
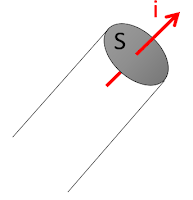
On considère une surface dS à travers laquelle se propage une onde sonore. Au passage de l'onde s'exerce sur les particules de fluide une force pressante dF=PdS. Pour calculer la puissance de cette force, on effectue le produit scalaire de la force par la vitesse, ce qui nous donne : \[\wp=P_{1}.\overrightarrow{v}.\overrightarrow{dS}\]On a bien un terme quadratique par rapport à une grandeur liée à l'onde.
On pose alors π le vecteur de Poynting acoustique, qui caractérise le propagation de l'énergie à travers une surface. Par définition : \[\overrightarrow{\pi}=P_{1}.\overrightarrow{v}\]π est homogène à une densité surfacique de puissance (en W.m^{-2})
On peut dès lors établir l'équation de conservation de l'énergie acoustique. En considérant un volume τ, limité par une surface fermée (Σ), on effectue un bilan d'énergie entre t et t+dt :
- Energie acoustique(t+dt) = Energie acoustique(t) + ce qui rentre - ce qui sort
\[\iiint_{\tau }^{ }e(M,t+dt)d\tau = \iiint_{\tau }^{ }e(M,t)d\tau -\oint_{\Sigma }^{ }\overrightarrow{\pi }.\overrightarrow{dS}dt\]
d'où :\[\iiint_{\tau }^{ }[e(M,t+dt)-e(M,t)]d\tau = -\iiint_{\tau }^{ }div(\overrightarrow{\pi})d\tau.dt\]
L'égalité suivante est donc vraie pour tout volume τ : \[\iiint_{\tau }^{ }[\frac{\partial e}{\partial t}+div(\overrightarrow{\pi})]d\tau =0\]
On obtient donc l'équation de conservation de l'énergie acoutisque : \[\frac{\partial e}{\partial t}+div(\overrightarrow{\pi})=0\]
