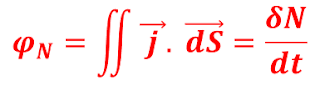Diffusion de particules

Le phénomène de diffusion se retrouve partout aujourd'hui, que ce soit pour homogéniser des solutions en laboratoire de chimie, parfumer une pièce, isoler un habitat, etc... 

Ce chapitre s'intéresse en particulier à la diffusion de particule dans un espace donné. Comment s'organise-t-elle ? Quelles lois permettent de la décrire ? Ou encore par quelle équation est-elle régit ?

Mais qu'est ce que la diffusion ?

Il s'agit d'un phénomène de transport sans mouvement macroscopique (ou mouvement d'ensemble) du support, tendant à uniformiser une grandeur (concentration, température, quantité de mouvement) d'un système initialement hors équilibre.

I - La loi phénoménologique de Fick

Avant de présenter la fameuse loi qui régit la diffusion de particule, il paraît nécessaire d'introduire quelques notions fondamentales.
Il faut premièrement introduire le nombre de particule passant de (1) à (2) à travers une surface orientée : nous l'appellerons dN.

Ce nombre de particule permet de définir le nombre de particule par unité de surface et par unité de temps. Il s'agit du vecteur densité de flux (ou de courant) de particule.

Ainsi, on peut définir le flux de particule, c'est-à-dire le nombre de particule traversant une surface orientée par unité de temps.

Mais comment s'opère la diffusion ? Expérimentalement, on peut effectuer plusieurs constats. Premièrement, la diffusion de particule ne s'opère que lorsqu'il existe une inhomogénéité de concentration dans le milieu. D'autre part, elle s'effectue dans un sens unique, des zones de forte concentration vers les zones de faible concentration.

C'est pourquoi, Adolf Fick énonce une loi phénoménologique (ie issue de diverses observations empiriques, et en accord avec la théorie, mais qui n'en est pas issue) qui portera son nom. Elle permet de décrire le flux surfacique de particules en énonçant que celui-ci est proportionnel au gradient de concentration.

Loi de Fick : 

Où n représente le nombre de particules par unité de volume.

Néanmoins, comme toute loi phénoménologique, celle-ci n'est pas toujours valable. Ainsi, on dénombre 4 hypothèses de validité nécessaires :
1 - Hypothèse d'un milieu isotrope pour avoir D indépendant de la direction de gradient de concentration
2 - Gradient de concentration pas trop important pour avoir une loi linéaire
3 - Milieu suffisamment dense pour être dans l'approximation des milieux continus
4 - Fluctuation "pas trop rapide" de n dans le temps pour avoir une réponse instantanée.